With an increased need for redundancy and fault tolerance in distributed computing a 40 years old question is more in focus than ever: how to build a self-replicating distributed fault tolerant system?
Paxos consensus algorithm
Perhaps the most widely-known consensus algorithm is the Paxos algorithm. Leslie Lamport first described Paxos algorithm for distributed consensus in 1990 (in a tech report that was widely considered to be a joke). The algorithm was finally published in 1998, and after the algorithm continued to be ignored (as it was purely in mathematical form), Lamport finally gave up and translated the results into readable English. It is now understood to be one of the most efficient practical algorithms for achieving consensus in a message-passing systems with failure detectors - mechanisms that allow nodes to give up on other stalled nodes after some amount of time (which can’t be done in a standard asynchronous system because giving up can be made to happen immediately by the adversary). The first version of the algorithm was a single version of Paxos that solves a single agreement problem. The version that is today more typically used is called a multi-Paxos and mainly uses repeated executions of the basic Paxos algorithm to implement a replicated state machine. There are many more variants of Paxos in use (called Fast Paxos, Cheap Paxos, Generalized Paxos, Byzantine Paxos, etc.).
The Paxos algorithm itself is pretty simple in its very nature, but it is not very intuitive. The algorithm itself is mostly concerned with guaranteeing agreement and validity while allowing for the possibility of termination if there is a long enough interval in which no nodes restart the protocol. Nodes are classified as proposers, accepters, and learners (a single node may have all three roles).
The idea is that a proposer attempts to ratify a proposed decision value (from an arbitrary input set) by collecting acceptances from a majority of the accepters, and the learners observe this ratification. The agreement is enforced by guaranteeing that only one proposal can get the votes of a majority of acceptors, and validity follows from only allowing input values to be proposed. The tricky part is ensuring that we don’t get a deadlock when there are more than two proposals or when some of the nodes fail. The intuition behind how this works is that any proposer can effectively restart the protocol by issuing a new proposal (thus dealing with lockups), and there is a procedure to release accepters from their old votes if we can prove that the old votes were for a value that won’t be getting a majority any time soon. To organize this vote-release process, we attach a distinct proposal number to each proposal. The safety properties of the algorithm don’t depend on anything but the proposal numbers being distinct, but since higher numbers override lower numbers, to make progress, we’ll need them to increase over time. The simplest way to do this in practice is to make the proposal number be a timestamp with the proposer’s ID appended to break ties. We could also have the proposer poll the other nodes for the most recent proposal number they’ve seen and add 1 to it.
In essence, the re-voting mechanism now works like this: before taking a vote, a proposer tests the waters by sending a prepare(n) message to all acceptors, where n is the proposal number. An acceptor responds to this with a promise never to accept any proposal with a number less than n (so that old proposals don’t suddenly get ratified) together with the highest-numbered proposal that the acceptor has accepted (so that the proposer can substitute this value for its own, in case the previous value was in fact ratified). If the proposer receives a response from a majority of the acceptors, the proposer then does the second phase of voting where it sends accept(n, value) to all acceptors and wins if receives a majority of votes. Note that acceptance is a purely local phenomenon. Additional messages are needed to detect which if a majority of acceptors has accepted any proposals. Typically this involves another round, where acceptors send accepted(n, value) to all learners (often just the original proposer), which can then notify everybody else if it doesn’t fail first. If the designated learner does fail first, we can restart by issuing a new proposal (which will get replaced by the previous successful proposal because of the safety properties). There is no requirement that only a single proposal is sent out (as if proposers can fail we will need to send out more to jump-start the protocol). The protocol guarantees agreement and validity no matter how many proposers there are and no matter how often they start.
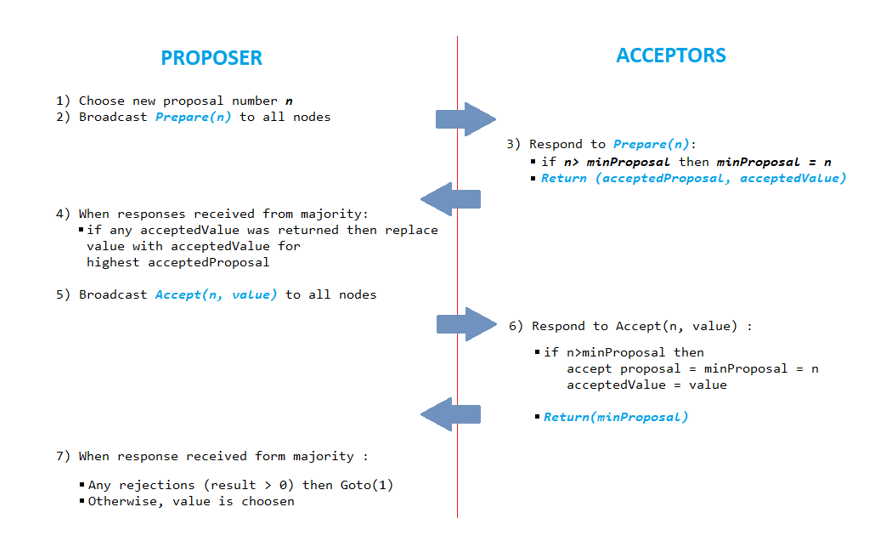
The protocol needs to terminate eventually so let’s suppose that there is a single proposer and that it survives long enough to collect a majority of acks and to send out accepts to a majority of the accepters. If everybody else cooperates, we can get termination in 4 message delays, including the time for the learners to detect acceptance. If there are multiple proposers, then they can step on each other. It’s enough to have two carefully synchronised proposers alternate sending out prepare messages to prevent any accepter from every accepting since an accepter promises not to accept accept(n, v) once it has responded to prepare(n + 1).
The solution is to ensure that there is eventually some interval during which there is precisely one proposer who doesn’t fail. One way to do this is to use Fibonacci or exponential random back-off when a proposer decides it’s not going to win a round (e.g. by receiving a nack or by waiting long enough to realize it won’t be getting any more acks soon), it picks some increasingly large random delay before starting a new round thus two or more will eventually start far enough apart in time that one will get done without interference. A more general solution is to assume some sort of weak leader election mechanism, which tells each accepter who the “legitimate” proposer is at each time.
The acceptors then discard messages from illegitimate proposers. That prevents conflict at the cost of possibly preventing progress. Progress is however obtained if the mechanism eventually reaches a state where a majority of the accepters bow to the same non-faulty proposer long enough for the proposal to go through. Such a weak leader election method is an example of a more general class of mechanisms known as failure detectors, in which each process gets hints about what other processes are faulty that eventually converge to reality.
Multi-Paxos and replicated state machine
The most common practical use of Paxos known today is to implement a replicated state machine. As we already know, the idea is to maintain many copies of some data structure, each on a separate machine, and guarantee that each copy (replica) stays in sync with all the others as new operations are applied to the state machine. To ensure that all the different replicas apply the same sequence of operations we require some additional mechanism, or in other words that the machines that hold the replicas solve a sequence of agreement problems to agree on these operations. The payoff is that the state of the data structure survives the failure of some of the machines, without having to copy the entire structure every time it changes.
Multi-Paxos (in some of its versions) uses a leader approach. Proposer (a leader) acts as a dispatcher for operations, and here Paxos works well as the agreement mechanism. A client app can contact the currently active node (leader, proposer) instead of having to broadcast operation to all replicas, and the proposer can include the operation in its next proposal. Further optimization of the algorithm allows skipping prepare and acknowledge messages in between agreement protocols for continuous operations if the proposer doesn’t change very often. This reduces the time to certify each operation to a single round-trip for accept and accepted messages.
To make this work, we need to distinguish between successive proposals by the same proposer and ‘new’ proposals that change the proposer in addition to reaching agreement on some value. This is done by splitting the proposal number into a major and minor number, with proposals ordered lexicographically. A proposer that wins {x, 0} is allowed to make further proposals numbered {x, 1}, {x, 2}, etc. but a different proposer will need to increment x.

